(Optimierung in der Strömungsmechanik)
Lecturer: Prof. Nicolas R. Gauger, Ole Burghardt
Date and Place:
Lectures and Exercises: usually Tuesdays and Wednesdays 8:30h, see exact timetable in the OpenOLAT repository.
Attention: The third lecture will take place on 2nd May 9:30h!
Seminar Room 32-349
ECTS: 4.5
SWS: V2Ü1
Language: English
OpenOLAT: Optimization in Fluid Mechanics
Audience:
Master students in mathematics and computer science. Preferably with some basic knowledge about PDEs and numerics.
Objective:
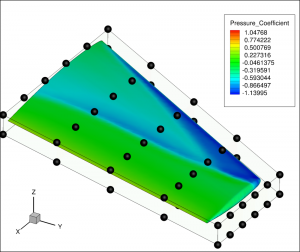
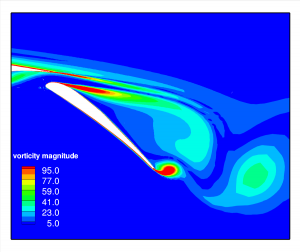
We will introduce and investigate methods for efficient numerical solutions to shape optimization problems in fluid mechanics and questions in optimal active flow control.
In the tutorial classes we will apply such methods to an airfoil design problem within the open-source solver SU2.
Content:
- Governing equations for fluid mechanics
- Reynolds-averging and turbulence modeling
- Finite volume method
- Objective functions and constraints
- Shape optimization in fluid mechanics
- Optimal active flow control
- Continuous and discrete adjoint methods
- One-shot methods
Literature:
- LeVeque, R.: Numerical Methods for Conservation Laws, Lectures in Mathematics. ETH Zürich
- Hirsch, C.: Numerical Computation of Internal and External Flows, Vol. 1 & 2, Wiley
- Blazek, J.: Computational Fluid Dynamics: Principles and Applications, Elsevier
- Mohammadi, B.; Pironneau, O.: Applied Shape Optimization for Fluids, Oxford University Press
- Griewank, A.; Walther, A.: Evaluating Derivatives, Principles and Techniques of Algorithmic Differentiation, Second Edition, SIAM
- Naumann, U.: The Art of Differentiating Computer Programs: An Introduction to Algorithmic Differentiation, SIAM