Algorithmic Differentiation in High-Energy Physics

Exploration of Differentiability

Algorithmic differentiation (AD) computes the accurate derivative at one particular point. Optimization benefits from AD gradients if they approximate the objective functions well in a larger neighborhoods. Using the example of a proton computed tomography (pCT) setup by the Bergen pCT collaboration involving a simulated human head and a digital tracking calorimeter, we have analyzed some algorithms from the high-energy physics (HEP) domain to determine whether they compute smooth functions.

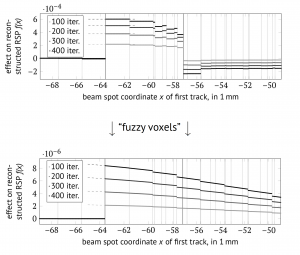
The fuzzy voxels approach makes (local) derivatives represent the global evolution of a CT output variable w.r.t. a CT input variable much better.

Common tomographic reconstruction algorithms involve many discrete operations to check whether proton paths have crossed image voxels or not; accordingly, the reconstructed pCT image reacts to changes in the inputs mostly via jumps. When the binary condition is relaxed into a “fuzzy voxels” approach based on distance, derivatives represent the global behavior much better.

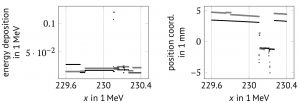
The Monte-Carlo simulation of the interaction of protons with the scanned object was done with GATE, a Geant4 application for medical imaging. We found that energy depositions in the detector are piecewise differentiable functions in the initial energy of the protons, but the jumps are much larger in magnitude than the continuous evolution in between the jumps.

Dependency of the energy deposition and a position coordinate on the primary energy, as simulated by GATE for a single particle.

Related publication: M. Aehle, J. Alme, G. Barnaföldi, J. Blühdorn, T. Bodova, V. Borshchov, A. van den Brink, V. Eikeland, G. Feofilov, C. Garth, N. R. Gauger, et al. Exploration of Differentiability in a Proton Computed Tomography Simulation Framework. Phys. Med. Biol. 68 (2023), 244002.

Tackling the Technical Challenge: Differentiating Geant4 with Derivgrind

The source code of GATE, together with the Geant4 toolkit and other dependencies, has more than one million lines. The technical challenge of differentiating such a large and complex codebase can be managed by using machine-code-based AD. After changing less than 20 lines of code to declare AD inputs and outputs and remove a “bit-trick”, our tool Derivgrind computes accurate derivatives of the energy depositions in the layers with respect to the primary energy. We verified this for the above pCT setup, simulating a single proton and comparing with difference quotients.

Related Publication: M. Aehle, L. Arsini, R. Belén Barreiro, A. Belias, F. Bury, S. Cebrian, A. Demin, J. Dickinson, J. Donini, T. Dorigo, M. Doro, N. R. Gauger, A. Giammanco, L. Gray, B. S. González, V. Kain, J. Kieseler, L. Kusch, et al. Progress in End-to-End Optimization of Detectors for Fundamental Physics with Differentiable Programming. arXiv:2310.05673 (2023).

Tackling the Mathematical Challenge: Smoother particle simulations

In practice, Geant4 simulations can involve many millions of particles. We are currently investigating whether Geant4 inputs affect statistical quantities like average energy depositions mainly through jumps (which would be non-differentiable and make AD gradients useless) or through differentiable evolution.