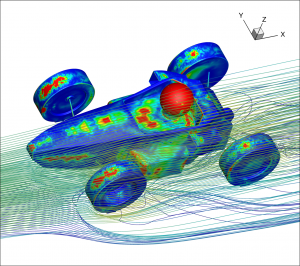
SU2 is a suite of open-source software tools written in C++ for the numerical solution of partial differential equations (PDE) and performing PDE constrained optimization. The primary applications are computational fluid dynamics and aerodynamic shape optimization, but has been extended to treat more general equations such as electrodynamics and chemically reacting flows.
- Under active development by Stanford University and by organizations all around the world (TU-KL, TU Delft, Imperial College London etc.)
- Comprises complete self-contained optimization environment
- Finite-Volume discretization of (U)RANS equations and turbulence models using a highly modular C++ code-structure
- Convergence acceleration using multi-grid and local time-stepping methods
- Several space (JST, Roe, AUSM etc.) and time integration methods (Explicit/Implicit Euler, Runge-Kutta)
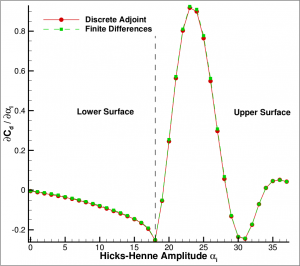
- Gradient computation using the Discrete Adjoint method or Continuous Adjoint method
- Integrated Algorithmic Differentiation (AD) support for derivative computations
At our group we are responsible for the development and maintenance of the AD based features printed in bold in the list above.
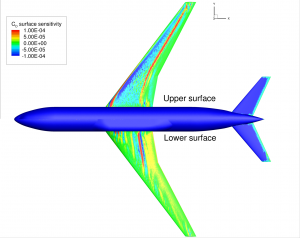
The implementation of the discrete adjoint solver is based on the reformulation of the optimization problem for state equations solved by fixed-point iterations. Leveraging the advantages of AD and the tool CoDiPack that makes use of modern meta programming techniques (also freely available as open-source), the resulting solver offers a efficient and flexible way of computing accurate gradients necessary for many different optimization problems. While the current version includes gradient computations for flows based on the steady Euler, Navier-Stokes and RANS equations (including turbulence models), later versions will also include unsteady problems, coupled problems (FSI, aeroacoustics etc.) and other problems that are right now or will be available for analysis in SU2. Since this approach also enables the rapid implementation of new discrete adjoint solvers, we are confident to have these features in the very near future.
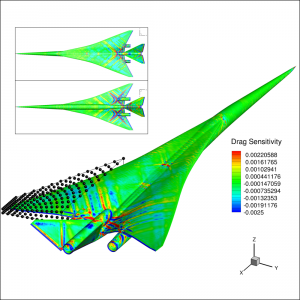
Drag surface sensitivity of the LM1021 supersonic passenger jet computed using the discrete adjoint method in SU2
The AD features along with the discrete adjoint solver are available in the recently released version 4.1 of SU2.
Information on how to install and use it will be added to the wiki on github soon!
Contact: Tim Albring and Prof. Nicolas R. Gauger.
Additional information and download:
Further applications