Goal: Learn how to define higher order types and how to compute higher order derivatives.

Prerequisite: Tutorial 2 - Reverse mode AD

Function: Simple real valued function for higher order derivatives

template<typename T>
T func(const T& x) {
  T t = x * x * x * x * x * x * x;
  return t * 3.0;
}

Full code:

using t1s = codi::RealForwardGen<double>;
using t2s = codi::RealForwardGen<t1s>;
using t3s = codi::RealForwardGen<t2s>;
using t4s = codi::RealForwardGen<t3s>;
using t5s = codi::RealForwardGen<t4s>;
using t6s = codi::RealForwardGen<t5s>;
 
using r6s = codi::RealReverseGen<t5s>;
 
template<typename T>
T func(const T& x) {
  T t = x * x * x * x * x * x * x;
  return t * 3.0;
}
 
int main() {
 
  {
    using DH = codi::DerivativeAccess<t2s>;
 
    t2s aFor = 2.0;
    // set all first order directions in order to get the 2. order derivative
    DH::setAllDerivatives(aFor, 1, 1.0);
 
    t2s cFor = func(aFor);
 
    std::cout << "t0s:   " << DH::derivative(cFor, 0, 0) << std::endl;
    std::cout << "t1_1s: " << DH::derivative(cFor, 1, 0) << std::endl;
    std::cout << "t1_2s: " << DH::derivative(cFor, 1, 1) << std::endl;
    std::cout << "t2s:   " << DH::derivative(cFor, 2, 0) << std::endl;
  }
 
  {
    using DH = codi::DerivativeAccess<t6s>;
 
    t6s aFor = 2.0;
 
    // set all first order directions in order to get the 6. order derivative
    DH::setAllDerivatives(aFor, 1, 1.0);
 
    t6s cFor = func(aFor);
 
    std::cout << "t0s: " << cFor << std::endl;
    std::cout << "t6s: " << DH::derivative(cFor, 6, 0) << std::endl;
  }
 
  {
    using DH = codi::DerivativeAccess<r6s>;
 
    r6s::Tape& tape = r6s::getTape();
    r6s aRev = 2.0;
    // set all first order directions on the primal value
    DH::setAllDerivativesForward(aRev, 1, 1.0);
 
    tape.setActive();
    tape.registerInput(aRev);
 
    r6s cRev = func(aRev);
 
    tape.registerOutput(cRev);
    // set all first order directions on the adjoint value
    DH::setAllDerivativesReverse(cRev, 1, 1.0);
 
    tape.setPassive();
    tape.evaluate();
 
    std::cout << "r0s: " << cRev << std::endl;
    std::cout << "r6s: " << DH::derivative(aRev, 6, 0) << std::endl;
 
    tape.reset();
  }
 
  return 0;
}

Defining higher order types

Higher order derivative types in CoDiPack can be defined by nesting the provided CoDiPack types. The simplest on is the nesting of forward types:

using t1s = codi::RealForwardGen<double>;
using t2s = codi::RealForwardGen<t1s>;
using t3s = codi::RealForwardGen<t2s>;
using t4s = codi::RealForwardGen<t3s>;
using t5s = codi::RealForwardGen<t4s>;
using t6s = codi::RealForwardGen<t5s>;

The types are created by using the general types where the user can specify the type of the value and gradient. The nesting is done in the example up to the 6-th order. This nesting is called forward-over-forward since the forward AD mode is applied on the forward AD mode.

The reverse types can also be used to create higher oder types. The general recomendation is to create first a nesing with forward mode types and then apply once the reverse type:

using r6s = codi::RealReverseGen<t5s>;

Here, a 6-th order type is constructed by applying five times the forward mode and then once the reverse mode. This nesting is called forward-over-reverse.

With these two techniques arbitray higher order types can be constructed. There are also the two other posibilites to use a reverse-over-forward nesting or a reverse-over-reverse nesting. The first one is mathematical identical to the forward-over-reverse approach but it would create a very large reverse tape since all higher order computations are recorded on the tape. The second approach is theoretical possible but the seccond application of the reversal transforms the reverse code into a forward derivative code. Therefore it is more appropritate to use a forward mode type in the first place.

Setting and getting derivatives

In order to know, which directions need to be set to get e.g. second order derivatives, the forward AD mode equation Forward AD Equation needs to be modified. (We use the notations from Uwe Naumans book "The Art of Differentiating Computer Programs".) Each application of the forward mode introduces a superscript with the number of the application. For the first application this is

$\dot w^{(1)} = d\phi/du * \dot u^{(1)} \eqdot$

The second application gets now the superscript 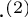$\cdot^{(2)}$ . Two superscirpts of the same mode are merged together. The total number of entries shows the derivative order of the value. The second application of the forward mode to the above equation yields (including all primal and derivative equations)

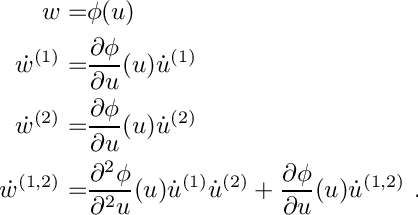
$\begin{align*} w =& \phi(u) \\ \dot w^{(1)} =& \frac{\d \phi}{\d u}(u) \dot u^{(1)} \\ \dot w^{(2)} =& \frac{\d \phi}{\d u}(u) \dot u^{(2)} \\ \dot w^{(1,2)} =& \frac{\d^2 \phi}{\d^2 u}(u) \dot u^{(1)} \dot u^{(2)} + \frac{\d \phi}{\d u}(u) \dot u^{(1,2)}\eqdot \end{align*}$

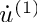
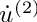
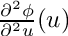
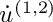
From these equations we learn, that all first order tangent directions $\dot u^{(1)}$ and $\dot u^{(2)}$ need to be set in order to get the second order derivative $\frac{\d^2 \phi}{\d^2 u}(u)$ . The second order tangent direction $\dot u^{(1,2)}$ needs to be zero, otherwise the result will contain additional information.

This can be extended to arbitrary derivative orders. All first order derivatives need to be seeded in order to compute the highest order derivative. For forward-over-reverse higher order types this is also true, but here n-1 direction need to be set during the recording and 1 direction during the reversal.

This tutorial uses the DerivativeAccess helper for the management of the derivative directions. It provides convinience functions that allow to set all derivatives on a specific order. For a compile time interface see the example Example 4 - Higher order derivatives compile time access. Example Example 5 - Higher order derivatives direct access shows how the gradients can be accessd without the helper.